BOJ : https://www.acmicpc.net/problem/1451
github : https://github.com/junho0956/Algorithm/blob/master/1451/1451/%EC%86%8C%EC%8A%A4.cpp
직사각형을 3군데로 나눌 수 있는 방법은 다음과 같다.
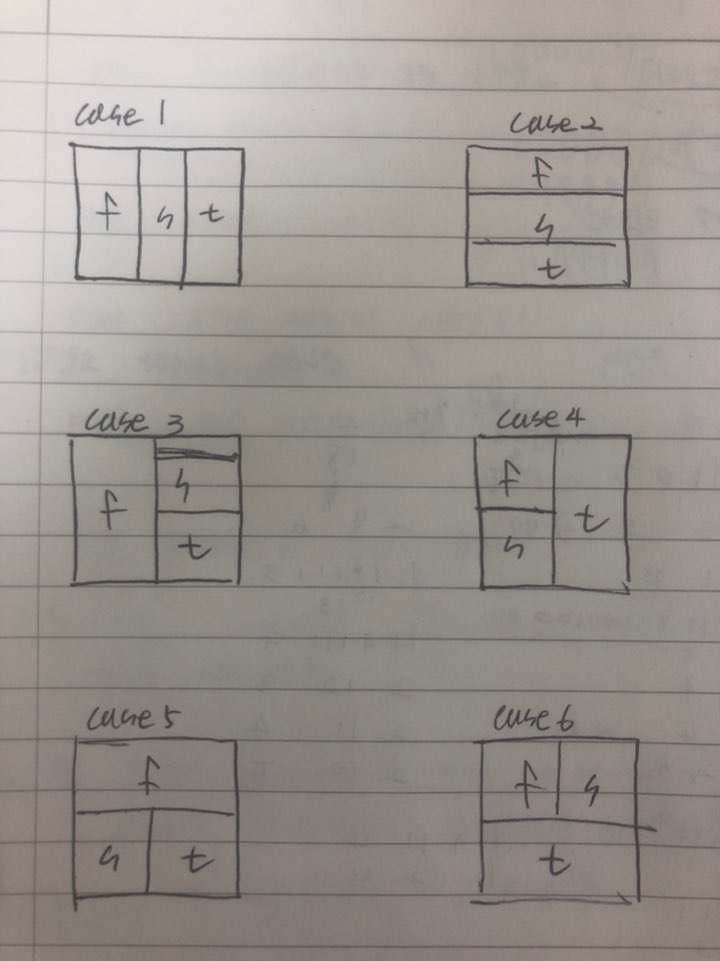
위의 6개 케이스가 나오게 되는데
이 경우를 반복문을 통해 합을 구해서 최댓값을 찾으면 된다.
임의의 fst 범위에 대한 값을 빠르게 구해와야 시간초과가 발생하지 않는다.
dp[i][k] = i행 k열 구간의 모든 수의 합이라고 가정할 때
dp[i][k] = dp[i-1][k] + dp[i][k-1] - dp[i-1][k-1] + this[i][k] 의 점화식으로 미리 계산해놓을 수 있으니
f s t 의 반복문 값만 잘 지정해주면 문제 없을 듯 하다.
더보기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
#include <cstdio>
#include <algorithm>
using namespace std;
#pragma warning(disable:4996)
int arr[101][101];
long long dp[101][101];
int main() {
int N, M;
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; i++) {
for (int k = 1; k <= M; k++) {
scanf("%1d", &arr[i][k]);
}
}
for (int i = 1; i <= N; i++)
for (int k = 1; k <= M; k++)
dp[i][k] = dp[i - 1][k] + dp[i][k - 1] - dp[i - 1][k - 1] + arr[i][k];
long long ans = 0;
long long f, s, t;
// case:1
for (int i = 1; i <= M - 2; i++) {
f = dp[N][i];
for (int k = i + 1; k <= M - 1; k++) {
s = dp[N][k] - f;
t = dp[N][M] - s - f;
ans = max(ans, f * s * t);
}
}
// case:2
for (int i = 1; i <= N - 2; i++) {
f = dp[i][M];
for (int k = i + 1; k <= N - 1; k++) {
s = dp[k][M] - f;
t = dp[N][M] - s - f;
ans = max(ans, f * s * t);
}
}
// case:3
for (int i = 1; i <= M - 1; i++) {
f = dp[N][i];
for (int k = 1; k <= N - 1; k++) {
s = dp[k][M] - dp[k][i];
t = dp[N][M] - f - s;
ans = max(ans, f * s * t);
}
}
// case:4
for (int i = 1; i <= M - 1; i++) {
for (int k = 1; k <= N - 1; k++) {
f = dp[k][i];
s = dp[N][i] - f;
t = dp[N][M] - f - s;
ans = max(ans, f * s * t);
}
}
// case:5
for (int i = 1; i <= N - 1; i++) {
f = dp[i][M];
for (int k = 1; k <= M - 1; k++) {
s = dp[N][k] - dp[i][k];
t = dp[N][M] - f - s;
ans = max(ans, f * s * t);
}
}
// case:6
for (int i = 1; i <= N - 1; i++) {
for (int k = 1; k <= M - 1; k++) {
f = dp[i][k];
s = dp[i][M] - f;
t = dp[N][M] - f - s;
ans = max(ans, f * s * t);
}
}
printf("%lld", ans);
return 0;
}
http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter
|
'algorithm > BOJ' 카테고리의 다른 글
| BOJ 10819번 차이를 최대로 (0) | 2020.01.22 |
|---|---|
| BOJ 2410번 2의 멱수의 합 (0) | 2020.01.22 |
| BOJ 1107번 리모컨 (0) | 2020.01.21 |
| BOJ 1476번 날짜 계산 (0) | 2020.01.17 |
| BOJ 1744번 수 묶기 (0) | 2020.01.17 |