과제를 하면서 알게된 방법을 적어보려고 한다

 

과제는 트리의 단말노드 <-> 단말노드 사이의 가중치 합에 대한 최댓값을 구하는 문제인데

처음에는 백준에서 풀었었던 트리의 지름(1967번, 1167번) 이 기억나서 

dfs 2번의 과정이면 충분히 해결할 수 있을거라고 생각하고 문제를 접근했다.

결과는 WA

 

트리의 지름의 경우 "임의의 노드"를 기준으로 하기 때문에 

단말노드와 단말노드 간의 거리를 구하기 위해 내부코드만 살짝 바꿔주었는데

뭔가 반례가 있나보다

단말노드 간의 정확한 계산은 dfs 을 2번 거치는 트리의지름 방법으로는 해결할 수 없다.

 

단말노드간의 정확한 계산방법을 풀이한다

계산방법은 "후위순회의 접근방법을 통한 자식을 관찰?하는 방법" 이다

후위 순회는 좌->우 자식을 전부 확인하고 자신을 확인하는 순회법이다

좌, 우 자식의 반환값을 통해 현재 노드의 정보를 갱신해가는 방법으로 해결할 수 있다.

 

다음의 트리를 기준으로 최댓값을 찾아보자

 

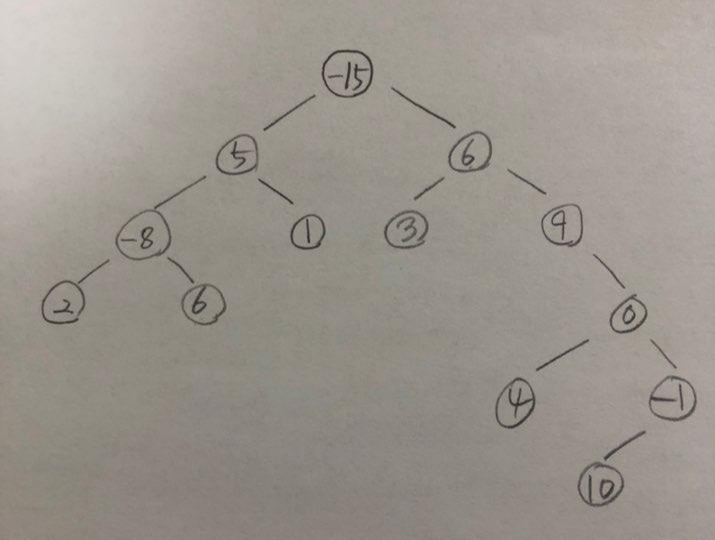
루트노드인 -15의 가중치를 가진 노드부터 시작해서

후위순회하듯이 좌측, 우측 자식의 반환값을 받을 것이다

반환값의 형태는 ( a, b ) 의 2개의 값을 가지는 한 쌍이다

 

( a, b ) 의 형태에서

a 는 두 자식중에서 큰 가중치를 골라 현재 가중치와 더하는

즉 현재노드의 자식에 위치한 단말노드까지의 최댓값을 의미하고

b 는 두 자식의 가중치와 현재 가중치를 모두 더하는

즉 현재노드의 자식에 위한 단말노드 간의 최댓값을 의미한다

 

좀더 간단하게 말하자면

a는 현재노드부터 좌/우 자식중 가장 큰 가중치를 갖는 경로,

b는 a를 통해 좌, 우자식을 둘다 연결하는 => 단말노드와 단말노드 간의 최댓값 경로가 된다

 

이 방법을 이용하여 -8 의 가중치를 갖는 노드의 리턴값을 예를 들면 다음과 같다

단말노드는 자식자체가 없기 때문에 가중치값을 쌍으로 반환하게 된다

비교대상은 항상 a(좌측) 값으로 이루어진다

2, 6 중에서 6이 크므로 -8과 더해서 a:-2 이라는 값이 만들어지고,

2, 6, -8을 더한 b:0 이라는 값이 만들어진다

이떄 -2는 -8 노드 기준 우측자식의 단말노드부터 현재노드까지의 최댓값을 의미하고

0은 -8 노드 기준 좌/우측 자식의 단말노드부터 현재노드까지의 최댓값을 의미하게 된다

 

이런식으로 재귀를 통해 다음과 같은 결과를 얻을 수 있다.

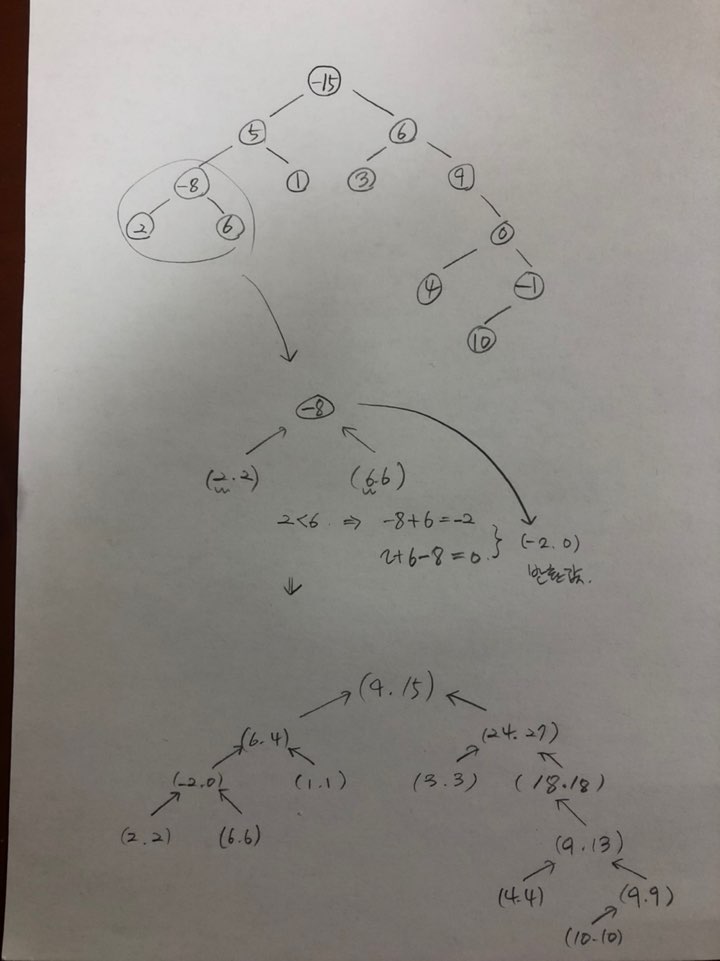
최댓값에 대한 비교는 항상 b로 이루어지고, 다음 결과를 통해 27이 정답이 됨을 알 수 있다

'algorithm > algorithm' 카테고리의 다른 글

위상 정렬(Topological Sort)  (0) 2020.06.22
강한 결합 요소 SCC(Strong connected component)  (0) 2020.06.22
전위 중위 후위 순회방법  (0) 2020.04.24
전위, 중위 정보로 트리 만들기  (0) 2020.04.24
c,c++ 세 점이 주어졌을 때 각도 구하기  (0) 2020.04.10

 

트리에서 전위 중위 후위 순회 하는 방법은 각 순회의 특징을 그대로 적용하는 것이다.

전위는 현재 노드를 먼저 읽는 방식으로 현재노드 -> 좌 -> 우

중위는 좌측 노드부터 먼저 읽는 방식으로 좌 -> 현재노드 -> 우

후위는 자식들을 전부 읽고 자신을 읽는 방식으로 좌 -> 우 -> 현재노드

 

이를 코드로 표현하면 다음과 같다

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
struct tree {
    int    w;
    tree* parent = NULL;
    tree* left = NULL;
    tree* right = NULL;
    bool visit = false;
};
 
void pre(tree* now) { // 전위
    if (now == NULL || now->visit) return;
 
    now->visit = true;
    cout << now->w << " ";
    pre(now->left);
    pre(now->right);
}
 
void in(tree* now) { // 중위
    if (now == NULL || now->visit) return;
    now->visit = true;
    in(now->left);
    cout << now->w << " ";
    in(now->right);
}
 
void post(tree* now) { // 후위
    if (now == NULL || now->visit) return;
    now->visit = true;
    post(now->left);
    post(now->right);
    cout << now->w << " ";
}
 
void solve() {
    
    cout << "pre : ";
    pre(root);
    for (int i = 0; i < tree_size; i++) node[i].visit = false;
    cout << "\n";
    cout << "in : ";
    in(root);
    for (int i = 0; i < tree_size; i++) node[i].visit = false;
    cout << "\n";
    cout << "post : ";
    post(root);
    for (int i = 0; i < tree_size; i++) node[i].visit = false;
}
 

 

다음과 같은 결과를 얻을 수 있다.

 

pre : 5 3 1 0 2 4 7 6 8 10 9 12 11 
in : 0 1 2 3 4 5 6 7 8 9 10 11 12 
post : 0 2 1 4 3 6 9 11 12 10 8 7 5 

'algorithm > algorithm' 카테고리의 다른 글

강한 결합 요소 SCC(Strong connected component)  (0) 2020.06.22
두 노드간의 최단or최장거리 찾기  (0) 2020.04.27
전위, 중위 정보로 트리 만들기  (0) 2020.04.24
c,c++ 세 점이 주어졌을 때 각도 구하기  (0) 2020.04.10
STL 사용할때 주의할 것(set,map,...)  (0) 2020.04.10

트리 변형 과제가 나온김에 포스팅해야겠다

 

임의의 트리에 대해서

전위와 중위 트리에 대한 정보가 주어졌을 떄 이 정보를 통해서 실제 트리를 구현해낼 수 있다.

 

단순히 재귀만 이용하면 되는 간단한 문제이다

 

전위, 중위 뿐만 아니라 중위, 후위 등등 최소 2개의 순서 정보만 있다면 실제 트리를 구현할 수 있다.

 

예를 들어 값 자체가 중위 순회 순서 값으로 이루어진 다음과 같은 트리를 보자

 

전위와 중위의 순서를 위 순서와 같다고 할 때 

다음과 같은 특징을 알 수 있다.

 

전위의 첫번째 값인 5는 곧 전체트리의 루트노드가 된다.

그럼 전체 트리중 5의 left 와 right는 어떻게 구별해야하나?

그것은 중위 순회의 순서에서 5를 찾아주면 된다.

결국 중위순회의 [0]~[4]번째까지는 5의 left 자식이 되고 [6]~[12]번째까지는 5의 right 자식이 된다

==> 전위 기준 [1]~[5]번째까지는 left의 자식, [6]~[12]번째까지는 5의 right 자식이 된다

 

결국 left, right를 나누는 기준은 전위, 중위의 배열 인덱스를 이용해서 현재 트리의 루트를 찾고 좌 우 를 나누는 것이다

 

이 특정 구간들을 다음과 같은 재귀문을 통해서 트리를 만들 수 있다.

 

order[] : 전위 순회의 순서가 들어간 배열

node[] : 중위 순회 순서의 값을 weight로 가지는 각 노드들

(node[]의 경우는 쉬운 예를 위해 이런식으로 표현한 것이고, 애초에 중위 순서가 주어진다면

이 순서를 배열에 넣고 사용하면 된다. 이 경우는 아예 값 자체를 중위 순회 순서로 넣은 것이니 착각하지말자)

1
2
3
4
5
6
7
8
9
void make_tree() {
    root = &node[order[0]];
 
    root->left = left_tree(0, order[0] - 1, 1);
    root->right = right_tree(order[0] + 1, tree_size - 1, order[0] + 1);
 
    if (root->left != NULL) root->left->parent = root;
    if (root->right != NULL) root->right->parent = root;
}
 

전역 변수 root는 order[0] (전위 순회의 첫번째 값) 을 루트노드로 가진다.

이 root의 left와 right에 다음과 같은 함수를 적용할 수 있다.

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
tree* right_tree(int l, int r, int idx) {
    return left_tree(l, r, idx);
}
 
tree* left_tree(int l, int r, int idx) {
    if (!(l <= r && idx < tree_size)) return NULL;
    tree* now = &node[order[idx]];
 
    if (l == r) return now;
 
    int next = order[idx];
    now->left = left_tree(l, next - 1, idx + 1);
    now->right = right_tree(next + 1, r, idx + (next - l) + 1);
 
    if (now->left != NULL) now->left->parent = now;
    if (now->right != NULL) now->right->parent = now;
 
    return now;
}
 

 

함수에서는 현재 노드를 루트로 보고 좌우의 트리를 반환받은 후에 루트노드를 리턴하는 형식이기 때문에 

결국 트리를 만드는 부분은 결국 left_tree 나 right_tree 가 같다고 볼 수 있다.

 

코드를 간단하게 설명하자면

중위 순회 : 0 1 2 3 4 5 6 7 ,,,

전위 순회 : 5 3 1 0 2 4 7 6 ... 

tree 함수는 다음과 같은 동작을 하게 된다

L,R 을 중위순회의 인덱스, idx 를 전위순회의 인덱스에 두고 좌 우를 찾게 된다

 

첫번째 left_tree를 기준으로

L : 0, R : 4, idx : 1 이다

order[idx] 는 3이 되고, 이 의미는 5의 좌측에 들어갈 루트노드가 3이 됨을 의미한다.

이 3을 중위 순회에서 몆번째 인덱스에 있는지 찾는다. (지금은 값 자체기 때문에 3이 된다)

중위 순회의 3번째 인덱스에 3이 있으므로, 3의 좌측에 들어갈 노드는

3 - 0(=> L이 0이므로) = 3개가 된다.

3의 좌측트리를 left_right(L, 3-1, idx+1) 의 반환값으로 호출 => 노드 0, 1, 2 를 3의 좌측트리에서 만든다

3의 우측트리를 right(3+1, R, idx+(3-L)+1) 의 반환값으로 호출 => 노드 4 를 3의 우측트리에서 만든다

 

다시 한번 말하지만

중위 순회를 0, 1, 2, 3, ... 순서대로 예를 든 것이기 때문에 L,R,next 같은 매개인자를 사용할 수 있는 것이고

애초에 이런식이 아닌 중위 순회의 값을 배열에 넣고 호출하는게 일반적일 것이다.

'algorithm > algorithm' 카테고리의 다른 글

두 노드간의 최단or최장거리 찾기  (0) 2020.04.27
전위 중위 후위 순회방법  (0) 2020.04.24
c,c++ 세 점이 주어졌을 때 각도 구하기  (0) 2020.04.10
STL 사용할때 주의할 것(set,map,...)  (0) 2020.04.10
Point in a Polygon - 다각형 내부점 판단  (0) 2020.04.07

BOJ : https://www.acmicpc.net/problem/1647

 

마을을 최소의 가중치를 가지는 간선으로 연결한 후에

다시 2개의 집합으로 나누어야 한다

문제의 조건에서 마을에는 최소 1개의 집만 있으면 된다고 하였으므로

어떤 간선이든 잘라도 이 조건이 유지된다

그러므로 MST로 연결된 모든 간선 중에서 가장 큰 가중치를 갖는 간선을 삭제해주면 답이된다

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <set>
#include <cmath>
#include <limits>
#include <cstring>
#include <string>
using namespace std;
 
typedef pair<int, int> pii;
vector<pii> v[100005];
bool visit[100005];
 
int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
 
    int N, M;
 
    cin >> N >> M;
    for (int i = 0; i < M; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        v[a].push_back({ c,b });
        v[b].push_back({ c,a });
    }
 
    priority_queue<pii, vector<pii>, greater<pii> > q;
    visit[1] = true;
    for (int i = 0; i < v[1].size(); i++) q.push({ v[1][i].first, v[1][i].second });
    int cnt = N - 1;
    long long ret = 0;
    int maxw = 0;
    while (cnt) {
        int w = q.top().first;
        int n = q.top().second;
        q.pop();
        if (visit[n]) continue;
        visit[n] = true;
        ret += w;
        cnt--;
        maxw = max(maxw, w);
        for (int i = 0; i < v[n].size(); i++) if (!visit[v[n][i].second]) q.push({ v[n][i].first, v[n][i].second });
    }
    cout << ret - maxw;
 
    return 0;
}
http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter

'algorithm > BOJ' 카테고리의 다른 글

BOJ 2194번 유닛 이동시키기 C++  (0) 2020.07.05
BOJ 14750번 Jerry and Tom  (0) 2020.04.28
BOJ 1922번 네트워크 연결  (0) 2020.04.11
BOJ 1197번 최소 스패닝 트리  (0) 2020.04.10
BOJ 2699번 격자점 컨벡스헐  (0) 2020.04.07

+ Recent posts

티스토리툴바