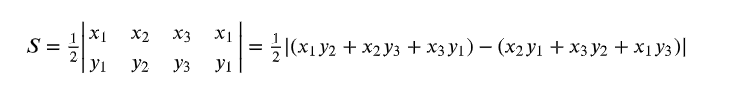BOJ : https://www.acmicpc.net/problem/1074
문제를 다시 풀어보았다.
분할정복, 말그대로 분할을 이용한 문제인 것 같다.
2*2 형태 부분만 찾으면 되기 때문에
분할은 다음과 같이 했다.
왼쪽상단을 fx, fy 라고하고 오른쪽하단을 ly, lx 라고가정
str 은 현재 왼쪽상단에 오게 될 숫자이고 num은 현재 오른쪽하단에 오게 될 숫자이다.
이때 4등분을 하게 되면 fx,fy,lx,ly 에 대한 위치를 분할해서 줄 수 잇을 것이며,
str, num 또한 위치에 맞게 분할해줄 수 있다.
2번이나 틀린 문제인데.. long long 을 사용하지 않아서 틀렸다.
2^15 의 좌표만 생각하고 int로만 했다가 WA을 받았다
숫자는 2^15 * 2^15 를 표현해야하니 longlong을 사용하자
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <set>
#include <cmath>
#include <limits>
using namespace std;
int N, r, c;
bool check;
void solve(int fy, int fx, int ly, int lx, long long str, long long num) {
if (check) return;
// 2*2 사이즈이면
if (ly - fy == 1 && lx - fx == 1) {
num--;
if (fy == r && fx == c) cout << num - 3;
if (fy == r && lx == c) cout << num - 2;
if (ly == r && fx == c) cout << num - 1;
if (ly == r && lx == c) cout << num;
check = true;
return;
}
// 범위를 n*n 기준 왼쪽위 1 오른쪽위2 왼쪽아래3 오른쪽아래4 로 가정하면
// r c 의 위치를 보고 분할한다
int midy = (fy + ly) / 2, midx = (fx + lx) / 2;
long long div = (num-str) / 4;
if (r <= midy && c <= midx) solve(fy, fx, midy, midx, str, num - (div * 3));
if (r <= midy && c > midx) solve(fy, midx+1, midy, lx, str+div, num - (div * 2));
if (r > midy && c <= midx) solve(midy + 1, fx, ly, midx, str+(div*2), num - div);
else solve(midy+1, midx+1, ly, lx, str+(div*3), num);
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> N >> r >> c;
r++, c++;
int len = pow(2, N);
solve(1, 1, len, len, 0, len*len);
return 0;
}
http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter
|
'algorithm > BOJ' 카테고리의 다른 글
| BOJ 3709번 레이저빔은 어디로 (0) | 2020.03.13 |
|---|---|
| BOJ 1043번 거짓말 (0) | 2020.03.13 |
| BOJ 1026번 보물 (0) | 2020.02.28 |
| BOJ 2240번 자두나무 (0) | 2020.02.26 |
| BOJ 1504번 특정한 최단 경로 (0) | 2020.02.24 |